Le sujet comporte quatre exercices répartis en deux pages

EXERCICE 1: (3 points)

I/Pour chacune des propositions suivantes, une seule des trois réponses est exacte. Indiquez la sans justifier.

𝜋    5

• Une racine carrée du nombre complexe (e 4 ) est :

𝜋

5𝜋

𝜋

1. e 4 b) e  8                                                                                                 c) e 8

• Soit a un réel non nul. On considère l’équation (E) : 𝑎. 𝑧² + 𝑧 + 𝑎 = 0. On note z′ et z′′

les solutions de l’équation (E), alors:

1. a) z^′ × z^′′ = − b) z^′ × z^′′ = ⁻¹

𝑎

1. c) z^′ × z^′′ = ¹

𝑎

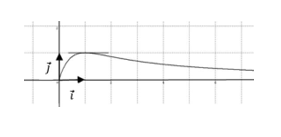
II/Soit ƒ une  fonction  deux  fois  dérivable  sur  [0, +∞[ et voici ci-contre la courbe de sa fonction dérivée ƒ′. Soit (C) la courbe représentative de la fonction ƒ.

Pour chacune des propositions suivantes, répondre par : vrai ou faux sans justifier :

• La fonction ƒ est décroissante sur [1, +∞[
• Le point d’abscisse 1 de (C) est un point d’inflexion de (C).

EXERCICE 2: (5 points)

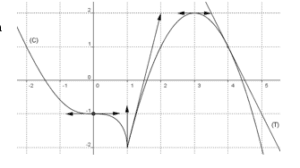
Dans le graphique ci-contre on a tracé dans un repère orthonormé (O,ı⃗,𝑗⃗) la courbe (C) d’une fonction ƒ définie sur IR.

ӿ (T) est la tangente à (C) au point A(4,1).

ӿ Chaque flèche représente un vecteur directeur d’une demi-tangente.

ӿ La courbe (C) admet exactement deux tangentes horizontales.

ӿ La courbe (C) admet deux branches paraboliques de direction celle de (O,𝑗⃗)

1) Déterminer : ƒ′(0)  , ƒ^′ (1) , ƒ′(3) , ƒ′(4)  ,         𝑙𝑚

(𝑥)+2

,       𝑙𝑚

(𝑥)

et      𝑙𝑚

(𝑥)

d                                                                                 𝑥⟶1−

𝑥−1

𝑥⟶+∞   𝑥

𝑥⟶−∞   𝑥

• Déterminer les intervalles sur lesquels ƒ est dérivable.
• Dresser le tableau de variation de la fonction ƒ et préciser les
• Soit la fonction 𝑔 définie sur ]−2,1[ par : 𝑔(𝑥) = ƒoƒ(𝑥)
  1. Déterminer ƒ(]−2,1[).
  2. Montrer que 𝑔 est dérivable sur ]−2,1[ puis écrire 𝑔^′(𝑥) à l’aide de ƒ′(𝑥) et ƒ(𝑥).
  3. En déduire le sens de variation de la fonction 𝑔 sur ]−2,1[.

EXERCICE 3: (6 points)

Soit ƒ la fonction définie sur [−1,1] par : ƒ(𝑥) = (1 − 𝑥)√1 − 𝑥2

• a) Etudier la dérivabilité de ƒ à droite en (-1) et à gauche en

1. b) Interpréter les résultats

• a) Montrer que ƒ est dérivable sur ]−1,1[ et que ƒ^′(𝑥) = 2𝑥2−𝑥−1 pour tout −1 < 𝑥 < 1

√1−𝑥2

1. b) Dresser le tableau de variation de ƒ. En déduire un encadrement de ƒ(𝑥).

3) On pose 𝑔(𝑥) = ƒ(𝑥) − 𝑥 pour tout 𝑥 ∈ [−1,1].

1. Montrer que l’équation 𝑔(𝑥) = 0 admet une unique solution 𝛼 dans l’intervalle ]0,1[.
2. En déduire que 𝛼 est une solution dans IR de l’équation : 𝑥⁴ − 2𝑥³ + 𝑥² + 2𝑥 − 1 = 0

EXERCICE 4: (6 points)

I/ 1) Résoudre dans ℂ l’équation (E) : 𝑧² − (1 + 3)𝑧 + 2 − 2 = 0

• Le plan complexe étant muni d’un repère orthonormé (, 𝑢⃗⃗, 𝑣⃗). On donne les points A,

B et D d’affixes respectives : 1 +   , 2 + 2   et   2

1. Déterminer l’affixe du point C tel que ABCD soit un parallélogramme.
2. Vérifier que z_B − z_A = −i(z_D − z_A)
3. En déduire que le parallélogramme ABCD est un carré.

II/ On considère dans ℂ l’équation (𝐸) : 𝑧² − (1 + 2 + 𝑐𝑠)𝑧 + 2 − 2𝑐𝑠 = 0    ;   ∈ [0, 𝜋]

• a) Vérifier que 𝑧₀ = 2 est une solution de l’équation (𝐸)

1. b) En déduire que l’autre solution de (𝐸) est 𝑧₁ = 1 + 𝑐𝑠

• Dans le plan complexe défini précédemment on donne les points K et M d’affixes

respectifs 𝑧_K =

et   𝑧_M = 1 + 𝑐𝑠.

Déterminer la valeur de  pour laquelle la distance KM est minimale.