Exercice n°1 🙁 4 points)

1. La durée de vie d’un robot, exprimée en années, jusqu’à ce que survienne la première panne est une variable aléatoire T qui suit une loi exponentielle de paramètre l , avec l >

• Déterminer l , arrondi à 10⁻¹ près sachant que la probabilité : P(T≤ 6) = 0,7.

Pour la suite de l’exercice, on prendra l = 0,2.

• Déterminer la valeur 𝑇₀ à un mois près vérifiant 𝑝(𝑇 ≥ 𝑇₀) = 0,5
• Sachant qu’un robot n’a pas eu de panne au cours des deux premières années, quelle est, à 10⁻² près, la probabilité qu’il soit encore en état de marche au bout de six ans ?

1. 1) Un revendeur commande un lot de 10 robots fonctionnant de manière indépendante. a)Déterminer la probabilité qu’il y ait au moins un robot ayantune durée de vie inférieure à 6 ans. b)Déterminer la probabilité qu’il y ait au plusdeux robotsayantune durée de vie inférieure à 6

• Le lot de 10 robots est réparti comme suit :8 robots de marque A et 2 de marque B mais ils sont emballés dans despaquets identiques donc on ne peut connaitre la marque que si on ouvre cet emballage.

Un client veut acheter un robot demarque A donc le revendeur va ouvrir les emballages un par un jusqu’à ce qu’il trouvelepremier robot demarque A.

Soit X la variable aléatoire qui prend pour valeur le nombre des packets ouverts jusqu’à ce qu’il apparait un robot demarque A pour la première fois .

On note P_n la probailité que le revendeur ouvre n packets pour qu’un robot demarque A apparaisse pour la première fois.

1. Vérifier que 1 ≤ 𝑛 ≤ 3

8                                      16

1. Montrer que𝑃₁ = 10et que𝑃₂ = 90

• Déterminer la loi de probabilité de X puis calculer son espérence.

Exercice n°2 : ( 4 points)

L’ampicilline est un antibiotique utilisé pour traiter les infections bactériennes.

Lorsqu’on l’injecte à un patient, la substance va s’infiltrer dans le réseau sanguin puis sera filtrée par les reins et le foie puis éliminée à une vitesse qui dépend de l’infection.

On injecte à un adulte malade une quantité de 500 mg et on note f(t) la quantité d’ampicilline restante dans le corps à l’instant t  exprimé en heure.

On sait que f(t) est une solution de l’équation différentielle (E) : y’ = ay où a est un réel.

• a) Résoudre dans [0, +∞[ l’équation différentielle (E) en fonction de

1. b) Déduire que 𝑓𝑓(𝑡) = 500𝑒^𝑎𝑡
2. c) Sachant que chez un adulte, 40% de l’antibiotique sera éliminé aprés une heure ,déterminer la valeur de a à 10^-1 prés.

• Dans la suite on prend a = – 0,5.
  1. Calculer la quantité restante après 3
  2. Au cours de quelle heure la quatité restante est égale à 40mg ?
  3. Sachant que l’antibiotique perd son efficacité si la quantité est inférieure à 9 mg , après combien d’heures le malade doit prendre la deuxième dose .( temps arrondi à l’unité)

Exercice n°3 : ( 5 points)

L’espace est muni d’un repère orthonormé direct ( 0, i, j, k ) . Soit les points A(1,2,-1) ,B(1,0,1) , C(2,1,-1).

• a) Calculer

AB Ù AC et déduire que A, B et C ne sont pas alignés.

1. b) Déterminer une équation cartésienne du plan P=(ABC).

• Soit S l’ensemble des points d’équation : x² + y² + z² =10.
  1. Monter que S est une sphère dont on précisera le rayon et le centre.
  2. Montrer que S et P sont sécants suivant un cercle (C) dont on précisera le rayon et le centre H.

𝑥 =  1 − 2 𝖺

• Soit Q le plan médiateur du segment [AB] et soit la droite∆: �𝑦 = 1+𝖺

𝑧 = 𝖺

𝖺∈ 𝐼𝑅

1. Montrer qu’une équation du plan Q est : y – z – 1 = 0
2. Vérifier que ∆ = 𝑃 ∩ 𝑄𝑄.
3. Déduire que pour tout point M de ∆ ona AM =BM.
4. Montrer qu’il existe deux points du cercle (C) tel que AM =BM dont on déterminera leurs coordonnées.

• Déduire qu’il existe un unique point D du cercle (C) telque ABD soit équilatéral.

4) Soit le point 𝑁(𝑐𝑜𝑠𝑐𝑐 + 𝑠𝑠𝑠𝑛𝑐𝑐 , −√8 , 𝑐𝑜𝑠𝑐𝑐 − 𝑠𝑠𝑠𝑛𝑐𝑐) où 𝑐𝑐 𝜖𝜖[0, 𝜋]

• Vérifier que N ∈

1. Montrer que le volume du tétraédre ABCN égale V = 3 [√8 + 2(1 − 𝑐𝑜𝑠𝑐𝑐)]

• Déterminer la valeur de 𝑐𝑐 pour que le volume V soit

Exercice n°4 : ( 7 points)

¹        𝑠𝑠𝑠 𝑥 ∈ ]0, +∞[

• Soit la fonction f définie sur l’ensemble]0, +∞[ par𝑓𝑓(𝑥) = �1+𝑥𝑙𝑛𝑥

𝑓𝑓(0) = 1

1. Monter que f est continue à droite de 0.
2. Etudier la dérivabilité de f à droite de 0 et interpréter graphiquement le résultat.

• Calculer lim_𝑥→+∞ 𝑓𝑓(𝑥)puis interpréter graphiquement le résultat. 2)a) Montrer que pour tout x∈ ]0, +∞[ : 𝑓𝑓^′ (𝑥) = ^{−1−𝑙𝑛𝑥}

1. b) Dresser le tableau de variation de

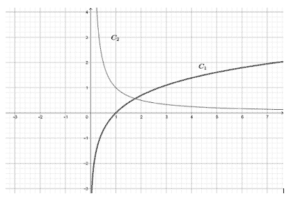
• Dans l’annexe ci-joint on atracé les courbes (C₁) et (C₂) des fonctions définies sur]0, +∞[

1

respectivement par𝑥 → 𝑙𝑛𝑥 𝑒𝑡 𝑥 →

𝑥

1. Construire le point A de (C₁) d’abscisse𝑒⁻¹et le point B de (C₂) d’abscisse1 − 𝑒⁻¹.
2. Déduire une construction du point C de la courbe (𝐶_𝑓𝑓 ) d’abscisse𝑒⁻¹.

• Soit la fonction g définie sur l’ensemble ]0, +∞[ par𝑔(𝑥) = 1 − 𝑥 + 𝑥𝑙𝑛𝑥.
  1. Etudier le sens de variations de
  2. Déduire que g(x) ≥ 0 et que pour tout x ϵ]0, +∞[ ona : 1 + 𝑥𝑙𝑛𝑥 ≥ 𝑥

1. Déduirequepour tout x ϵ]0, +∞[ :𝑓𝑓(𝑥)≤ ¹

𝑥

puis donner la position de (𝐶_𝑓𝑓 ) 𝑒𝑡 (𝐶₂).

1. Tracer dans l’annexe la courbe (𝐶_𝑓𝑓 ).

• Soit 𝖺 un réel de [1, +∞[,on note A(𝖺) l’aire de la partie du plan limitée par (𝐶_𝑓𝑓 ) , l’axe des abscisses et les droites d’équations x =1 et x =𝖺

1. Montrer que pour tout 𝑥 ∈ [1, +∞[ 𝑜𝑛 𝑎 :

1

𝑥+𝑥𝑙𝑛𝑥

≤ 𝑓𝑓(𝑥) ≤ ¹

𝑥

1

1. b) Déduire que : ln⁡(1 + 𝑙𝑛 𝖺) ≤ 𝐴(𝖺) ≤ 𝑙𝑛 𝖺. ( On remarque que : 1   =     ^𝑥     )

1. c) Déduire lim_𝖺→+∞ 𝐴(𝖺)

𝑥+𝑥𝑙𝑛𝑥

1+𝑙𝑛𝑥